1. 数组元素的赋值
/*
* 打印杨辉三角
*
* */
public class ArrayExer2 {
public static void main(String[] args) {
// 1 声明并初始化二维数组
int[][] yangHui = new int[10][];
// 2 给数组元素赋值
for (int i = 0; i < yangHui.length; i++) {
yangHui[i] = new int[i + 1];
yangHui[i][0] = 1;
yangHui[i][i] = 1;
for (int j = 1; j < yangHui[i].length - 1; j++) {
yangHui[i][j] = yangHui[i - 1][j] + yangHui[i - 1][j - 1];
}
}
// 3 遍历
for (int i = 0; i < yangHui.length; i++) {
for (int j = 0; j < yangHui[i].length; j++) {
System.out.print(yangHui[i][j] + "\t");
}
System.out.println();
}
}
}运行结果:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1
2. 求数值型数组中元素的最大值、最小值、平均值、平均数、总和等
/*
* 算法考察:求数值型数组中元素的最大值、最小值、平均数、总和等
*
* 定义一个int型的一维数组,包含10个元素,分别赋一些随机整数,然后求出所有元素最大值、最小值、和值平均值并输出
* 要求:所有随机数都是两位数
* */
public class ArrayTest1 {
public static void main(String[] args) {
int[] arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * (99 - 10 + 1) + 10);
System.out.print(arr[i] + "\t");
}
System.out.println();
// 求最大值
int maxValue = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > maxValue) {
maxValue = arr[i];
}
}
System.out.println("最大值为:" + maxValue);
// 求最小值
int minValue = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i];
}
}
System.out.println("最小值为:" + minValue);
// 求和
int sum = 0;
for (int i = 0; i < arr.length; i++) {
sum += arr[i];
}
System.out.println("总和为:" + sum);
// 求平均值
System.out.println("平均值为:" + (sum / arr.length));
}
}
运行结果:
10 99 42 72 18 80 23 72 76 18 最大值为:99 最小值为:10 总和为:510 平均值为:51
3. 数组的复制、反转、查找(线性查找、二分法查找)
public class ArrayTest2 {
public static void main(String[] args) {
String[] arr = new String[] { "AA", "BB", "CC", "DD", "EE", "FF" };
// 输出arr
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + "\t");
}
System.out.println("以上是原始数组");
// 数组的复制
String[] arr1 = new String[arr.length];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = arr[i];
}
// 输出arr1
for (int i = 0; i < arr1.length; i++) {
System.out.print(arr1[i] + "\t");
}
System.out.println("以上是复制后的arr1");
// 数组的反转
for (int i = 0; i < arr1.length / 2; i++) {
String temp = arr1[i];
arr1[i] = arr1[arr1.length - i - 1];
arr1[arr1.length - i - 1] = temp;
}
// 输出arr1
for (int i = 0; i < arr1.length; i++) {
System.out.print(arr1[i] + "\t");
}
System.out.println("以上是原地反转后的arr1");
// 查找(搜索)
// 线性查找:依次遍历查找
String dest = "BB";
boolean flag = false;
for (int i = 0; i < arr.length; i++) {
if (dest.equals(arr[i])) {
System.out.println("找到了指定元素\"" + dest + "\", 索引位置:" + i);
flag = true;
break;
}
}
if (flag == false) {
System.out.println("没有查找到结果");
}
// 二分查找(较快, 前提是数组必须有序)
int[] arr2 = new int[] { -98, -90, -20, 0, 1, 4, 65, 76, 98 };// 目标查找数组
int dest1 = -21;
int head = 0;
int end = arr2.length - 1;
boolean flag2 = false;
while (head <= end) {
int middle = (head + end) / 2;
if (dest1 == arr2[middle]) {
System.out.println("找到了指定元素\"" + dest1 + "\", 索引位置:" + middle);
flag2 = true;
break;
} else if (arr2[middle] > dest1) {
end = middle - 1;
} else {
head = middle + 1;
}
}
if (flag2 == false) {
System.out.println("没有查找到结果");
}
}
}
运行结果:
AA BB CC DD EE FF 以上是原始数组 AA BB CC DD EE FF 以上是复制后的arr1 FF EE DD CC BB AA 以上是原地反转后的arr1 找到了指定元素"BB", 索引位置:1 没有查找到结果
4. 数组元素的排序算法
4.1 排序算法的概念
排序:假设含有n个记录的序列为{R1, R2, R3, ..., Rn},其相应关键字序列为{K1, K2, K3, ..., Kn}。将这些记录重新排序为{Ri1, Ri2, Ri3, ..., Rin},使得相应的关键字值满足条件Ki1 <= Ki2 <= Ki3 ... <= Kin,这样的操作称为排序
衡量排序算法的优劣:
- 时间复杂度:分析关键字比较次数和记录的移动次数
- 空间复杂度:分析排序算法中需要的辅助内存
- 稳定性:若两个记录
A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种排序算法是稳定的。
4.2 排序算法的分类
- 内部排序:整个排序过程不需要借助外部存储器(如硬盘等),所有排序操作都在内存中完成。
- 外部排序:参与排序的数据非常多,数据量庞大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(如磁盘)。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成的。
4.3 十大排序算法
选择排序
直接选择排序
堆排序

交换排序
冒泡排序
快速排序
插入排序
直接插入排序
- 折半插入排序
Shell排序
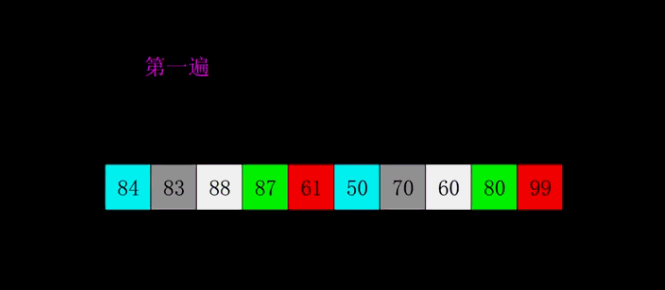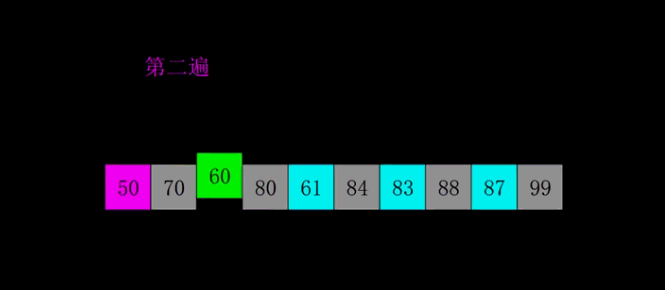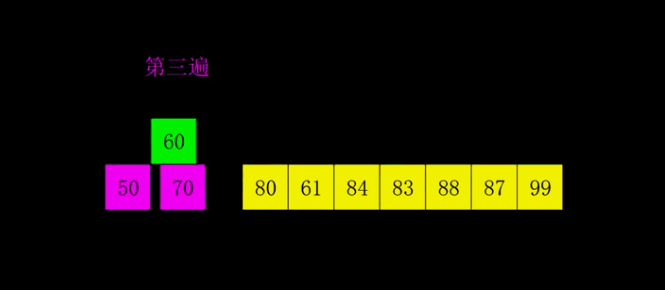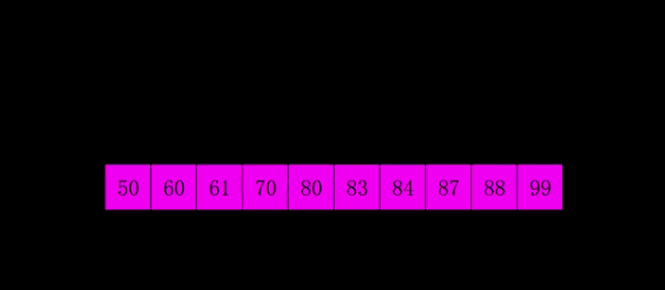
归并排序
桶式排序
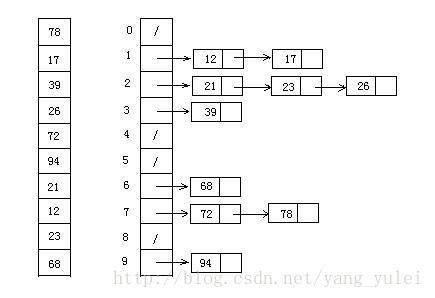
基数排序

每种算法都有其对应的实现思想,运行效率和适用范围也各不相同,之后的文章中将单独进行介绍,本文只描述冒泡排序和快速排序。
4.4 算法的五大特征
- 输入(Input):有0个或多个输入数据,这些数据必须有清楚的描述和定义。
- 输出(Output):至少有一个或多个输出结果。
- 有穷性(有限性,Finiteness):算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成。
- 确定性(明确性,Definiteness):算法中的每一步都有明确的含义,不会出现二义性。
- 可行性(有效性,Effectiveness):算法的每一步都是清楚可行的,能让用户纸笔计算而求出答案。
满足确定性的算法也称为 “确定性算法” 。现在人们也会关注更加广泛的概念,例如考虑各种非确定性算法,如并行算法、概率算法等。另外,人们也关注并不要求终止的计算描述,这种描述有时被称为 “过程(procedure)”
4.5 冒泡排序和快速排序
4.5.1. 冒泡排序
- 介绍:冒泡排序的原理非常简单,它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
排序思想:
- 比较相邻的元素。如果第一个比第一个大(升序),就交换它们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越小的元素重复上面的步骤,直到没有任何一对数字需要比较为止。
/* * 冒泡排序实现 * * */ public class BubbleSort { public static void main(String[] args) { int[] arr = new int[] { 43, 32, 76, -98, 0, 64, 33, -21, 32, 99 }; // 冒泡排序 for (int i = 0; i < arr.length - 1; i++) { for(int j = 0;j<arr.length - 1- i;j++) { if(arr[j]>arr[j+1]) { int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } } for(int i = 0; i<arr.length;i++) { System.out.print(arr[i]+"\t"); } System.out.println(); } }
运行结果:
-98 -21 0 32 32 33 43 64 76 9
4.5.2.快速排序- 介绍:快速排序通常明显比同为O(nlogn)的其它算法更快,因此常被采用,而且快速排序采用了分治法的思想,所以在很多笔试面试中经常能看到快速排序的影子。可见快速排序的重要性。
- 快速排序是迄今为止所有内排序算法中速度最快的一种。是交换排序的一种。
排序思想:
- 从数列中跳出一个元素,称为“基准”。
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准大的摆在基准后面(相同的数可放到任意一侧)。在这个分区结束后,该基准值就处于数列的中间位置。称这个为“分区操作”。
- 递归地把小于基准值元素的子数列和大于基准值的元素的子数列排序。
- 递归的最后情形,是数列的的大小是零或一,也就是永远都已经被排序了。虽然一直递归下去,但是这个算法总会结束,因为在每次迭代中,它至少会把一个元素摆到它最后的位置去。
/**
* 快速排序
*/
public class QuickSort {
private static void swap(int[] data, int i, int j) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
private static void subSort(int[] data, int start, int end) {
if (start < end) {
int base = data[start];
int low = start;
int high = end + 1;
while (true) {
while (low < end && data[++low] - base <= 0)
;
while (high > start && data[--high] - base >= 0)
;
if (low < high) {
swap(data, low, high);
} else {
break;
}
}
swap(data, start, high);
subSort(data, start, high - 1);//递归调用
subSort(data, high + 1, end);
}
}
public static void quickSort(int[] data){
subSort(data,0,data.length-1);
}
public static void main(String[] args) {
int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
quickSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
运行结果:
排序之前: [9, -16, 30, 23, -30, -49, 25, 21, 30] 排序之后: [-49, -30, -16, 9, 21, 23, 25, 30, 30]
4.6 排序算法总结
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(n1.3) | O(n2) | O(n) | O(1) | 不稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 |
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(nlog2n) | 不稳定 |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n2) | O(n) | O(n+k) | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
5. Arrays 工具类的使用
import java.util.Arrays;
/*
* Arrays数组工具类的使用
* */
public class ArraysTest {
public static void main(String[] args) {
int[] arr1 = new int[] { 1, 2, 3, 4 };
int[] arr2 = new int[] { 1, 3, 4, 2 };
int[] arr3 = new int[] { -30, 3, 42, 56, 78, 10 };
// 1. equals()
System.out.println("equals():" + arr1.equals(arr2));
// 2. toString()
System.out.println("toString():" + Arrays.toString(arr1));
// 3. fill()
Arrays.fill(arr1, 10);
System.out.println("fill():" + Arrays.toString(arr1));
// 4. sort()
Arrays.sort(arr2);
System.out.println("sort():" + Arrays.toString(arr2));
// 5. binarySearch()
int index = Arrays.binarySearch(arr3, 3);
if (index > 0) {
System.out.println("找到了");
} else {
System.out.println("没找到");
}
}
}
运行结果:
equals():false toString():[1, 2, 3, 4] fill():[10, 10, 10, 10] sort():[1, 2, 3, 4] 找到了
6. 数组使用中的常见异常
6.1. 数组角标越界异常
int[] arr = new int[] {1,2,3,4,5};
for(int i = 0;i<=arr.length;i++) {//引用了索引 ‘5’
System.out.println(arr[i]);
}导致异常:
java.lang.ArrayIndexOutOfBoundsException
6.2. 空指针异常
int[] arr = new int[] { 1, 2, 3, 4, 5 };
arr = null;
System.out.println(arr[0]);// 引用了空指针导致异常:
java.lang.NullPointerException

